Introduction
Navier-Stokes equations (NSE), governing the motion of a viscous fluid, are used in various applications: from simulations of the flow in blood vessels to studies of the air flow around aeroplane wings and rotor blades, scaling up to models of ocean and atmospheric currents. Even in the case of an incompressible steady flow, NSE are non-linear due to the effect of the inertia, which is more pronounced in case of a higher Reynolds number. In this tutorial we discuss the implementation of a viscous fluid model in MoFEM using hierarchical basis functions. This approach permits us to locally increase the order of approximation, enforcing conformity across finite element boundaries, without the need to change the implementation of an element. Moreover, the requirement of different approximation orders for primal (velocity) and dual (pressure) variables, necessary for a simulation of the flow using the mixed formulation, can be easily satisfied.
Problem statement
An incompressible isoviscous steady-state flow in a domain \(\Omega\) is governed by the following equations:
\[
\begin{align}
\label{eq:balance_momentum} \rho \left(\mathbf{u}\cdot\nabla\right)\mathbf{u} - \mu\nabla^2\mathbf{u} + \nabla p &= \mathbf{f},\\
\label{eq:cont} \nabla\cdot\mathbf{u} &= 0,
\end{align}
\]
where \eqref{eq:balance_momentum} is the set of Navier-Stokes equations, representing the balance of the momentum, and \eqref{eq:cont} is the continuity equation; \(\mathbf{u}=[u_x, u_y, u_z]^\intercal\) is the velocity field, \(p\) is the hydrostatic pressure field, \(\rho\) is the fluid mass density, \(\mu\) is fluid viscosity and $\mathbf{f}$ is the density of external forces. The boundary value problem complements the above equations by the Dirichlet and Neumann conditions on the boundary \(\partial\Omega\):
\[
\begin{align}
\label{eq:bc_d}\mathbf{u} = \mathbf{u}_D & \;\text{on}\; \Gamma_D,\\
\label{eq:bc_n}\mathbf{n}\cdot \left[-p\mathbf{I}+\mu\left(\nabla\mathbf{u} + \nabla\mathbf{u}^\intercal\right)\right] = \mathbf{g}_N & \;\text{on} \;\Gamma_N,
\end{align}
\]
where \(\mathbf{u}_D\) is the prescribed velocity on the part of the boundary \(\Gamma_D\subset\partial\Omega\), and \(\mathbf{g}_N\) is the prescribed traction vector on the part of the boundary \(\Gamma_N\subset\partial\Omega\), \(\mathbf{n}\) is an outward normal.
In this tutorial we will solve the problem of the fluid flow around a rigid sphere (see Figure 1) of a radius \(r\) positioned in the centre of a cubic domain, the side length \(2l\) of which is considered sufficiently large compared to \(r\), so that a uniform far-field velocity on the exterior boundaries is valid (note that the body forces are neglected). Exploiting the symmetry of the problem, we will use a quarter of the domain in our simulations.
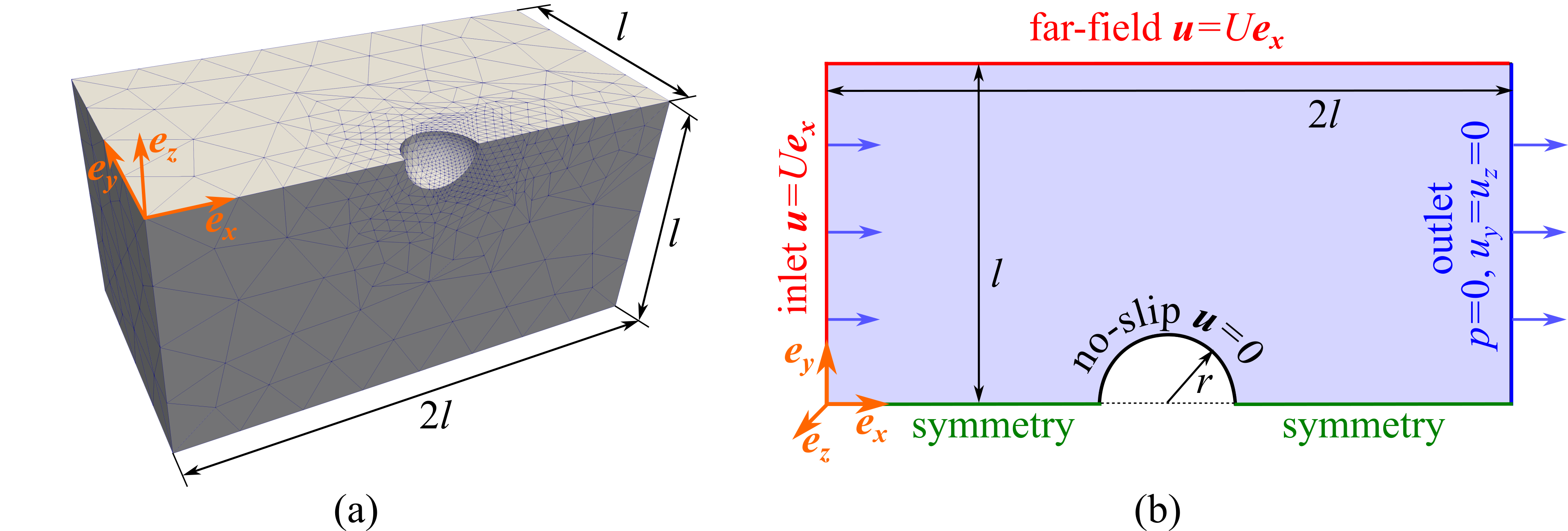
Figure 1: (a) Finite-element mesh used for simulation of fluid flow around a rigid sphere. (b) Sketch of the problem set-up on a section $z=0$ of the mesh.
Note that due to the structure of differential operators in the Navier-Stokes equations \eqref{eq:balance_momentum}, the fluid pressure has to be specified on a part of boundary in order to obtain a unique solution. To achieve that, we will combine Dirichlet and Neumann condition on the outlet boundary of the domain, see see Figure 1. In the case when the flow is perpendicular to the boundary ( \(u_y = u_z = 0\)), which is enforced by the Dirichlet boundary condition, the hydrostatic fluid pressure equals to the normal traction on such boundary, see Theorem 1 in [barth2007boundary].
Non-dimensionalization and scaling
Reynolds number is introduced for the problems governed by the Navier-Stokes equations as a measure of the ratio of inertial forces to viscous forces:
\[
\begin{equation}
\mathcal{R} = \frac{\rho U L }{\mu},
\end{equation}
\]
where \(U\) is the scale for the velocity and \(L\) is a relevant length scale. For the problem of the fluid flow around a sphere, considered in this tutorial, the far-field velocity plays the role of the velocity scale, while \(L=2r\), where \(r\) is the radius of the sphere.
When viscous forces dominate over the inertia forces, \(\mathcal{R} \ll 1\), the non-linear term in \eqref{eq:balance_momentum} can be neglected, simplifying NSE down to Stokes equations. However, often this is not the case, i.e. the nonlinear term may become dominant over the viscous forces. In these cases non-dimensionalization (scaling) of Navier-Stokes equations is very useful, which permits to decrease the number of coefficients to only one – Reynolds number \(\mathcal{R}\). The following scales can be used for the case of flow with relatively low Reynolds number (e.g. less than 100).
Non-dimensionalization of Navier-Stokes equations
| Physical quantity | Scale | Dimensionless variable |
| Length | \(L\) | \(\mathbf{x}^{*}=\mathbf{x}\:/\:L, \quad \nabla^{*}(\cdot) = L\nabla(\cdot)\) |
| Velocity | \(U\) | \(\mathbf{u}^{*}=\mathbf{u}\:/\:U\) |
| Pressure | \(P=\frac{\mu U}{L}\) | \(p^{*}=p\:/\:P\) |
Mote that the scale for pressure depends on the scales for the length and the velocity. Using these scales, Navier-stokes equations (1) - (2) can be written in the following dimensionless form (considering zero external forces):
\[
\begin{align}
\label{eq:balance_momentum_dim_less} \mathcal{R} \left(\mathbf{u}^{*}\cdot\nabla^{*}\right)\mathbf{u}^{*} - (\nabla^{*})^2\mathbf{u}^{*} + \nabla^{*} p^{*} &= 0,\\
\label{eq:cont_dim_less} \nabla^{*}\cdot\mathbf{u}^{*} &= 0,
\end{align}
\]
Note that now the influence of the non-linearity (inertia terms) on the problem is fully controlled by the value of the Reynolds number. On the one hand, if \(\mathcal{R} \ll 1\), or if one simply wants to consider the Stokes equation, the nonlinear term can be dropped. On the other hand, if the Reynolds number is sufficiently high, then the non-linearity can become strong and may pose problems for convergence (see below discussion of the linearisation of the problem for the Newton-Raphson method). In this case a certain iterative procedure can be used to obtain a solution. Indeed, to find the solution for a given Reynolds number, a number of intermediate problems can be solved for range of smaller \(\mathcal{R}\), eventually reaching the original value. Such technique will also be used in this tutorial. Note also that below we will drop the * symbol, implying that during computation all considered quantities are dimensionless, and a transformation to the dimensional variables is performed before post-processing of the results takes place.
Finite-element formulation
Weak form
The weak statement of the problem \eqref{eq:balance_momentum}-\eqref{eq:bc_n} reads: Find a vector field \(\mathbf{u} \in \mathbf{H}^1(\Omega)\) and a scalar field \(p \in L^2(\Omega)\), such that for any test functions \(\mathbf{v} \in \mathbf{H}^1_0(\Omega)\) and \(q \in L^2(\Omega)\):
\[
\begin{align}
\label{eq:weak}
\mathcal{R}\int\limits_\Omega \left(\mathbf{u}\cdot\nabla\right)\mathbf{u} \cdot\mathbf{v} \,d\Omega + \int\limits_{\Omega}\nabla\mathbf{u}\mathbin{:}\nabla\mathbf{v}\, d\Omega - \int\limits_{\Omega}p\, \nabla\cdot\mathbf{v} \, d\Omega &= \int\limits_{\Omega}\mathbf{f}\cdot\mathbf{v}\,d\Omega + \int\limits_{\Gamma_N}\mathbf{g}_N\cdot\mathbf{v}\,d\Gamma_N,\\
- \int\limits_{\Omega}q\, \nabla\cdot\mathbf{u} \, d\Omega &= 0
\end{align}
\]
Upon finite-element discretization of the domain \(\Omega\), we consider interpolation of both unknown fields introducing shape functions on each element: \begin{equation} \label{eq:shape} u_i = \sum\limits_{\alpha=1}^{n_{\mathbf{u}}} N_{\alpha}\, u_i^\alpha, \quad p = \sum\limits_{\beta=1}^{n_p} \Phi_{\beta}\, p^\beta; \quad v_i = \sum\limits_{\alpha=1}^{n_{\mathbf{u}}} N_{\alpha}\, v_i^\alpha, \quad q = \sum\limits_{\beta=1}^{n_p} \Phi_{\beta}\, q^\beta, \end{equation} where \(n_{\mathbf{u}}\) is the number of shape functions associated with the velocity field, and $n_p$ is the similar number for the pressure field. Using the hierarchical basis approximation, the vector of the shape functions can be decomposed into four sub-vectors, consisting of shape functions associated with element's entities: vertices, edges, faces and the volume of the element, e.g. for the velocity field:
\[
\begin{equation}
\label{eq:shape_hier}
\mathbf{N}^\textit{el} = \left[N_1, \ldots N_\alpha, \ldots N_{n_{\mathbf{u}}}\right]^\intercal = \left[\mathbf{N}^\textit{ver}, \mathbf{N}^\textit{edge}, \mathbf{N}^\textit{face}, \mathbf{N}^\textit{vol}\right]^\intercal.
\end{equation}
\]
Note on the choice of spaces for the mixed problem
Note that in the weak statement velocity and pressure fields belong to different spaces: \(H^1\) and \(L^2\), respectively. Two different approaches can be used for implementing such mixed formulation in the finite-element framework. One can use generalised Taylor-Hood elements, which feature continuous ( \(H^1\) ) approximation of both velocity and pressure fields, however, in order to enforce stability, the approximations functions for the pressure field should be one order lower than those for the velocity field. Furthermore, Taylor-Hood elements impose certain constraints on the mesh, see [wieners2003taylor]. Alternatively, a discontinuous approximation for pressure can be used, however, in this case the difference between the orders of approximation functions for velocity and for pressure should be 2.
Implementation
The example class has necessary fields to store input parameters and internal data structures, as well as a set of functions for setting up and solving the problem:
commonData = boost::make_shared<NavierStokesElement::CommonData>(m_field);
}
}
private:
boost::shared_ptr<NavierStokesElement::CommonData>
commonData;
boost::shared_ptr<VolumeElementForcesAndSourcesCore>
feLhsPtr;
boost::shared_ptr<VolumeElementForcesAndSourcesCore>
feRhsPtr;
boost::shared_ptr<FaceElementForcesAndSourcesCore>
feDragPtr;
boost::shared_ptr<VolumeElementForcesAndSourcesCoreOnSide>
feDragSidePtr;
};
#define CHKERR
Inline error check.
PetscErrorCode MoFEMErrorCode
MoFEM/PETSc error code.
std::bitset< BITREFLEVEL_SIZE > BitRefLevel
Bit structure attached to each entity identifying to what mesh entity is attached.
Deprecated interface functions.
MoFEMErrorCode setupElementInstances()
[Setup algebraic structures]
MoFEMErrorCode setupDiscreteManager()
[Define finite elements]
boost::shared_ptr< FaceElementForcesAndSourcesCore > feDragPtr
MoFEMErrorCode defineFiniteElements()
[Setup fields]
boost::shared_ptr< PostProcFace > fePostProcDragPtr
boost::shared_ptr< VolumeElementForcesAndSourcesCore > feLhsPtr
MoFEMErrorCode setupFields()
[Find blocks]
MoFEMErrorCode setupSNES()
[Setup element instances]
MoFEMErrorCode runProblem()
[Example Navier Stokes]
boost::shared_ptr< NavierStokesElement::CommonData > commonData
boost::shared_ptr< DirichletDisplacementBc > dirichletBcPtr
PetscBool isDiscontPressure
MoFEMErrorCode setupAlgebraicStructures()
[Setup discrete manager]
boost::shared_ptr< VolumeElementForcesAndSourcesCoreOnSide > feDragSidePtr
MoFEMErrorCode findBlocks()
[Read input]
boost::shared_ptr< VolumeElementForcesAndSourcesCore > feRhsPtr
boost::ptr_map< std::string, NeumannForcesSurface > neumannForces
MoFEM::Interface & mField
boost::shared_ptr< PostProcVol > fePostProcPtr
MoFEMErrorCode solveProblem()
[Setup SNES]
MoFEMErrorCode postProcess()
[Solve problem]
MoFEMErrorCode readInput()
[Run problem]
The set of functions used in this tutorials in the following:
}
#define MoFEMFunctionBegin
First executable line of each MoFEM function, used for error handling. Final line of MoFEM functions ...
#define MoFEMFunctionReturn(a)
Last executable line of each PETSc function used for error handling. Replaces return()
The function ExampleNavierStokes::runProblem is executed from the main function:
int main(
int argc,
char *argv[]) {
const char param_file[] = "param_file.petsc";
try {
moab::Core mb_instance;
moab::Interface &moab = mb_instance;
}
return 0;
}
#define CATCH_ERRORS
Catch errors.
static MoFEMErrorCode Initialize(int *argc, char ***args, const char file[], const char help[])
Initializes the MoFEM database PETSc, MOAB and MPI.
static MoFEMErrorCode Finalize()
Checks for options to be called at the conclusion of the program.
Reading mesh and input parameters
The workflow of solving a problem using the finite-element method starts from reading the mesh and other input parameters:
PetscBool flg_mesh_file;
PetscOptionsBegin(PETSC_COMM_WORLD, "", "NAVIER_STOKES problem",
"none");
CHKERR PetscOptionsString(
"-my_file",
"mesh file name",
"",
"mesh.h5m",
CHKERR PetscOptionsBool(
"-my_is_partitioned",
"is partitioned?",
"",
CHKERR PetscOptionsInt(
"-my_order_u",
"approximation orderVelocity",
"",
CHKERR PetscOptionsInt(
"-my_order_p",
"approximation orderPressure",
"",
CHKERR PetscOptionsInt(
"-my_num_ho_levels",
"number of higher order boundary levels", "",
CHKERR PetscOptionsBool(
"-my_discont_pressure",
"discontinuous pressure",
"",
CHKERR PetscOptionsBool(
"-my_ho_geometry",
"use second order geometry",
"",
CHKERR PetscOptionsScalar(
"-my_velocity_scale",
"velocity scale",
"",
CHKERR PetscOptionsInt(
"-my_step_num",
"number of steps",
"",
numSteps,
PetscOptionsEnd();
if (flg_mesh_file != PETSC_TRUE) {
SETERRQ(PETSC_COMM_SELF, 1, "*** ERROR -my_file (MESH FILE NEEDED)");
}
const char *option;
option = "PARALLEL=READ_PART;"
"PARALLEL_RESOLVE_SHARED_ENTS;"
"PARTITION=PARALLEL_PARTITION;";
} else {
const char *option;
option = "";
}
}
virtual moab::Interface & get_moab()=0
virtual MoFEMErrorCode rebuild_database(int verb=DEFAULT_VERBOSITY)=0
Clear database and initialize it once again.
MoFEMErrorCode getInterface(IFACE *&iface) const
Get interface reference to pointer of interface.
Once the mesh is read, we find the set of tetrahedra corresponding to the computational domain. Furthermore, we identify the fluid-structure interface, i.e. the set of triangles corresponding to the surface of the sphere:
if (
bit->getName().compare(0, 9,
"MAT_FLUID") == 0) {
const int id =
bit->getMeshsetId();
bit->getMeshset(), 3,
commonData->setOfBlocksData[
id].eNts,
true);
std::vector<double> attributes;
bit->getAttributes(attributes);
if (attributes.size() < 2) {
"should be at least 2 attributes but is %d",
attributes.size());
}
commonData->setOfBlocksData[id].fluidViscosity = attributes[0];
commonData->setOfBlocksData[id].fluidDensity = attributes[1];
}
}
if (
bit->getName().compare(0, 9,
"INT_SOLID") == 0) {
const int id =
bit->getMeshsetId();
bit->getMeshset(), MBTRI,
commonData->setOfFacesData[
id].eNts,
true);
commonData->setOfFacesData[
id].eNts, 3,
true, tets,
moab::Interface::UNION);
tet =
Range(tets.front(), tets.front());
if (
bit.second.eNts.contains(tet)) {
bit.second.fluidViscosity;
commonData->setOfFacesData[id].fluidDensity =
bit.second.fluidDensity;
break;
}
}
if (
commonData->setOfFacesData[
id].fluidViscosity < 0) {
"Cannot find a fluid block adjacent to a given solid face");
}
}
}
}
@ MOFEM_DATA_INCONSISTENCY
#define _IT_CUBITMESHSETS_BY_SET_TYPE_FOR_LOOP_(MESHSET_MANAGER, CUBITBCTYPE, IT)
Iterator that loops over a specific Cubit MeshSet having a particular BC meshset in a moFEM field.
Setting up fields, finite elements and the problem itself
Once the domain and the fluid-structure interface are identified, we can setup the problem. First, we define the velocity and pressure fields. Note that for velocity we use space H1, while for pressure the user can choose between using also H1 space (continuous approximation, Taylor-Hood element), or a discontinuous approximation using L2 space. Note that in the former case, the approximation functions for pressure has to be one order lower than that of the velocity (e.g. order 2 for velocity and order 1 for pressure), while the the latter case the difference between the two has to be 2 orders (e.g. order 3 for velocity and order 1 for pressure).
Furthermore, the properties of hierarchical basis functions can be used to locally increase the approximation order for the elements on the fluid-structure interface, where the gradients of the velocity can be expected to be the highest due to the no-slip boundary condition on the surface of the sphere.
} else {
}
3);
}
for (auto d : {1, 2, 3}) {
moab::Interface::UNION);
}
levels[ll] = subtract(ents, ents.subset_by_type(MBVERTEX));
}
levels[ll] = subtract(levels[ll], levels[ll - 1]);
}
int add_order = 1;
levels[ll]);
else
++add_order;
}
}
moab::Interface::UNION);
}
"VELOCITY");
"PRESSURE");
"MESH_NODE_POSITIONS");
}
Projection10NodeCoordsOnField ent_method_material(
mField,
"MESH_NODE_POSITIONS");
}
@ AINSWORTH_LEGENDRE_BASE
Ainsworth Cole (Legendre) approx. base .
@ L2
field with C-1 continuity
virtual MoFEMErrorCode build_fields(int verb=DEFAULT_VERBOSITY)=0
virtual MoFEMErrorCode add_ents_to_field_by_dim(const Range &ents, const int dim, const std::string &name, int verb=DEFAULT_VERBOSITY)=0
Add entities to field meshset.
virtual MoFEMErrorCode set_field_order(const EntityHandle meshset, const EntityType type, const std::string &name, const ApproximationOrder order, int verb=DEFAULT_VERBOSITY)=0
Set order approximation of the entities in the field.
virtual MoFEMErrorCode loop_dofs(const Problem *problem_ptr, const std::string &field_name, RowColData rc, DofMethod &method, int lower_rank, int upper_rank, int verb=DEFAULT_VERBOSITY)=0
Make a loop over dofs.
virtual MoFEMErrorCode add_field(const std::string name, const FieldSpace space, const FieldApproximationBase base, const FieldCoefficientsNumber nb_of_coefficients, const TagType tag_type=MB_TAG_SPARSE, const enum MoFEMTypes bh=MF_EXCL, int verb=DEFAULT_VERBOSITY)=0
Add field.
After that the finite elements operating on the set above fields can be defined. In particular, we define elements for solving Navier-Stokes equations, computation of the drag traction and force on the surface of the surface, and, finally, for computing the contribution of Neumann (natural) boundary conditions.
"PRESSURE", "MESH_NODE_POSITIONS");
}
virtual MoFEMErrorCode build_finite_elements(int verb=DEFAULT_VERBOSITY)=0
Build finite elements.
virtual MoFEMErrorCode build_adjacencies(const Range &ents, int verb=DEFAULT_VERBOSITY)=0
build adjacencies
static MoFEMErrorCode addElement(MoFEM::Interface &m_field, const string element_name, const string velocity_field_name, const string pressure_field_name, const string mesh_field_name, const int dim=3, Range *ents=nullptr)
Setting up elements.
Once the finite elements are defined, we will need to create element instances and push necessary operators to their pipelines. First, we setup an element for solving Navier-Stokes (or if one prefers, Stokes) equations. Note that right-hand side and left-hand side elements are considered separately. In case of Navier-Stokes equations, operators are pushed to elements pipelines using function NavierStokesElement::setNavierStokesOperators. In particular, the following operators are pushed to right-hand side:
while for the left-hand side we push these operators:
Upon that, we setup in the same way elements for computing the drag traction and the drag force acting on the sphere using operators NavierStokesElement::OpCalcDragTraction and NavierStokesElement::OpCalcDragForce, respectively. Additionally, operators for the Neumann boundary conditions are set using the function MetaNeumannForces::setMomentumFluxOperators and the element for the Dirichlet boundary conditions is created as well. Finally, operators for post-processing output are created: in the volume and on the fluid-solid interface.
feLhsPtr = boost::shared_ptr<VolumeElementForcesAndSourcesCore>(
new VolumeElementForcesAndSourcesCore(
mField));
feRhsPtr = boost::shared_ptr<VolumeElementForcesAndSourcesCore>(
new VolumeElementForcesAndSourcesCore(
mField));
true);
true);
feDragPtr = boost::shared_ptr<FaceElementForcesAndSourcesCore>(
feDragSidePtr = boost::shared_ptr<VolumeElementForcesAndSourcesCoreOnSide>(
new VolumeElementForcesAndSourcesCoreOnSide(
mField));
true);
} else {
}
"NAVIER_STOKES", "VELOCITY",
NULL, "VELOCITY");
true);
auto v_ptr = boost::make_shared<MatrixDouble>();
auto grad_ptr = boost::make_shared<MatrixDouble>();
auto pos_ptr = boost::make_shared<MatrixDouble>();
auto p_ptr = boost::make_shared<VectorDouble>();
new OpCalculateVectorFieldValues<3>("VELOCITY", v_ptr));
new OpCalculateVectorFieldGradient<3, 3>("VELOCITY", grad_ptr));
new OpCalculateScalarFieldValues("PRESSURE", p_ptr));
new OpCalculateVectorFieldValues<3>("MESH_NODE_POSITIONS", pos_ptr));
using OpPPMap = OpPostProcMapInMoab<3, 3>;
{{"PRESSURE", p_ptr}},
{{"VELOCITY", v_ptr}, {"MESH_NODE_POSITIONS", pos_ptr}},
{{"VELOCITY_GRAD", grad_ptr}},
{}
)
);
fePostProcDragPtr = boost::make_shared<PostProcFace>(mField);
fePostProcDragPtr->getOpPtrVector().push_back(
new OpCalculateVectorFieldValues<3>("MESH_NODE_POSITIONS", pos_ptr));
fePostProcDragPtr->getOpPtrVector().push_back(
fePostProcDragPtr->getPostProcMesh(),
fePostProcDragPtr->getMapGaussPts(),
{},
{{"MESH_NODE_POSITIONS", pos_ptr}},
{},
{}
)
);
fePostProcDragPtr, feDragSidePtr, "NAVIER_STOKES", "VELOCITY", "PRESSURE",
commonData);
}
MoFEMErrorCode addHOOpsVol(const std::string field, E &e, bool h1, bool hcurl, bool hdiv, bool l2)
OpPostProcMapInMoab< SPACE_DIM, SPACE_DIM > OpPPMap
Set Dirichlet boundary conditions on displacements.
Post post-proc data at points from hash maps.
Set integration rule to volume elements.
static MoFEMErrorCode setCalcDragOperators(boost::shared_ptr< FaceElementForcesAndSourcesCore > dragFe, boost::shared_ptr< VolumeElementForcesAndSourcesCoreOnSide > sideDragFe, std::string side_fe_name, const std::string velocity_field, const std::string pressure_field, boost::shared_ptr< CommonData > common_data)
Setting up operators for calculating drag force on the solid surface.
static MoFEMErrorCode setPostProcDragOperators(boost::shared_ptr< PostProcFace > postProcDragPtr, boost::shared_ptr< VolumeElementForcesAndSourcesCoreOnSide > sideDragFe, std::string side_fe_name, const std::string velocity_field, const std::string pressure_field, boost::shared_ptr< CommonData > common_data)
Setting up operators for post processing output of drag traction.
static MoFEMErrorCode setNavierStokesOperators(boost::shared_ptr< VolumeElementForcesAndSourcesCore > feRhs, boost::shared_ptr< VolumeElementForcesAndSourcesCore > feLhs, const std::string velocity_field, const std::string pressure_field, boost::shared_ptr< CommonData > common_data, const EntityType type=MBTET)
Setting up operators for solving Navier-Stokes equations.
static MoFEMErrorCode setStokesOperators(boost::shared_ptr< VolumeElementForcesAndSourcesCore > feRhs, boost::shared_ptr< VolumeElementForcesAndSourcesCore > feLhs, const std::string velocity_field, const std::string pressure_field, boost::shared_ptr< CommonData > common_data, const EntityType type=MBTET)
Setting up operators for solving Stokes equations.
Note that the class for enforcing Dirichlet boundary conditions DirichletDisplacementBc used in the snippet above requires the algebraic data structures for storing components of the right-hand side vector, left-hand side matrix and the solution vector. Therefore, these data structures need to be created beforehand using PETSc:
CHKERR VecGhostUpdateBegin(
F, INSERT_VALUES, SCATTER_FORWARD);
CHKERR VecGhostUpdateEnd(
F, INSERT_VALUES, SCATTER_FORWARD);
CHKERR VecGhostUpdateBegin(
D, INSERT_VALUES, SCATTER_FORWARD);
CHKERR VecGhostUpdateEnd(
D, INSERT_VALUES, SCATTER_FORWARD);
CHKERR MatSetOption(
Aij, MAT_SPD, PETSC_TRUE);
}
auto createDMVector(DM dm)
Get smart vector from DM.
auto createDMMatrix(DM dm)
Get smart matrix from DM.
SmartPetscObj< Vec > vectorDuplicate(Vec vec)
Create duplicate vector of smart vector.
However, one may note that creation of PETSCc vectors and matrices requires the instance of the MoFEM Discrete Manager (DM), which needs a certain setup as well:
DMType dm_name = "DM_NAVIER_STOKES";
}
PetscErrorCode DMMoFEMSetIsPartitioned(DM dm, PetscBool is_partitioned)
PetscErrorCode DMMoFEMAddElement(DM dm, std::string fe_name)
add element to dm
PetscErrorCode DMMoFEMCreateMoFEM(DM dm, MoFEM::Interface *m_field_ptr, const char problem_name[], const MoFEM::BitRefLevel bit_level, const MoFEM::BitRefLevel bit_mask=MoFEM::BitRefLevel().set())
Must be called by user to set MoFEM data structures.
PetscErrorCode DMRegister_MoFEM(const char sname[])
Register MoFEM problem.
virtual bool check_finite_element(const std::string &name) const =0
Check if finite element is in database.
Finally, the last preparatory step required is the setup of the SNES functionality:
boost::ptr_map<std::string, NeumannForcesSurface>::iterator mit =
&mit->second->getLoopFe(), NULL, NULL);
}
boost::shared_ptr<FEMethod> null_fe;
null_fe);
null_fe);
null_fe);
SnesCtx *snes_ctx;
}
PetscErrorCode DMMoFEMSNESSetFunction(DM dm, const char fe_name[], MoFEM::FEMethod *method, MoFEM::BasicMethod *pre_only, MoFEM::BasicMethod *post_only)
set SNES residual evaluation function
PetscErrorCode DMMoFEMSNESSetJacobian(DM dm, const char fe_name[], MoFEM::FEMethod *method, MoFEM::BasicMethod *pre_only, MoFEM::BasicMethod *post_only)
set SNES Jacobian evaluation function
PetscErrorCode DMMoFEMGetSnesCtx(DM dm, MoFEM::SnesCtx **snes_ctx)
get MoFEM::SnesCtx data structure
PetscErrorCode SnesMat(SNES snes, Vec x, Mat A, Mat B, void *ctx)
This is MoFEM implementation for the left hand side (tangent matrix) evaluation in SNES solver.
PetscErrorCode SnesRhs(SNES snes, Vec x, Vec f, void *ctx)
This is MoFEM implementation for the right hand side (residual vector) evaluation in SNES solver.
Solving the problem and post-processing the results
auto scale_problem = [&](
double U,
double L,
double P) {
"MESH_NODE_POSITIONS");
ProjectionFieldOn10NodeTet ent_method_on_10nodeTet(
mField,
"MESH_NODE_POSITIONS",
true,
true);
ent_method_on_10nodeTet.setNodes = false;
};
CHKERR PetscPrintf(PETSC_COMM_WORLD,
"Density: %6.4e\n",
density);
CHKERR PetscPrintf(PETSC_COMM_WORLD,
"Velocity scale: %6.4e\n",
CHKERR PetscPrintf(PETSC_COMM_WORLD,
"Pressure scale: %6.4e\n",
CHKERR PetscPrintf(PETSC_COMM_WORLD,
"Re number: 0 (Stokes flow)\n");
} else {
CHKERR PetscPrintf(PETSC_COMM_WORLD,
"Re number: %6.4e\n",
}
while (
lambda < 1.0 - 1e-12) {
bit.second.inertiaCoef = 0.0;
bit.second.viscousCoef = 1.0;
}
} else {
bit.second.viscousCoef = 1.0;
}
}
PETSC_COMM_WORLD,
"Step: %d | Lambda: %6.4e | Inc: %6.4e | Re number: %6.4e \n",
step,
CHKERR VecGhostUpdateBegin(
D, INSERT_VALUES, SCATTER_FORWARD);
CHKERR VecGhostUpdateEnd(
D, INSERT_VALUES, SCATTER_FORWARD);
CHKERR VecGhostUpdateBegin(
D, INSERT_VALUES, SCATTER_FORWARD);
CHKERR VecGhostUpdateEnd(
D, INSERT_VALUES, SCATTER_FORWARD);
}
}
PetscErrorCode DMoFEMMeshToGlobalVector(DM dm, Vec g, InsertMode mode, ScatterMode scatter_mode)
set ghosted vector values on all existing mesh entities
PetscErrorCode DMoFEMPreProcessFiniteElements(DM dm, MoFEM::FEMethod *method)
execute finite element method for each element in dm (problem)
{
std::ostringstream stm;
stm <<
"out_" <<
step <<
".h5m";
CHKERR PetscPrintf(PETSC_COMM_WORLD,
"Write file %s\n",
}
auto get_vec_data = [&](auto vec, std::array<double, 3> &data) {
const double *array;
CHKERR VecGetArrayRead(vec, &array);
}
CHKERR VecRestoreArrayRead(vec, &array);
};
std::array<double, 3> pressure_drag;
std::array<double, 3> shear_drag;
std::array<double, 3> total_drag;
"Pressure drag force: [ %6.4e, %6.4e, %6.4e ]",
pressure_drag[0], pressure_drag[1], pressure_drag[2]);
"Shear drag force: [ %6.4e, %6.4e, %6.4e ]", shear_drag[0],
shear_drag[1], shear_drag[2]);
"Total drag force: [ %6.4e, %6.4e, %6.4e ]", total_drag[0],
total_drag[1], total_drag[2]);
}
{
std::ostringstream stm;
stm <<
"out_drag_" <<
step <<
".h5m";
CHKERR PetscPrintf(PETSC_COMM_WORLD,
"out file %s\n",
}
}
#define MOFEM_LOG_C(channel, severity, format,...)
PetscErrorCode DMoFEMLoopFiniteElements(DM dm, const char fe_name[], MoFEM::FEMethod *method, CacheTupleWeakPtr cache_ptr=CacheTupleSharedPtr())
Executes FEMethod for finite elements in DM.
FTensor::Index< 'i', SPACE_DIM > i
virtual int get_comm_rank() const =0
Running the example
We will consider two cases: first, flow governed by Stokes equation, i.e. neglecting the nonlinear terms, and then we will solve full set Navier-Stokes equations. For both cases we will use the same mesh. We will start by partitioning this mesh:
mofem_part -my_file sphere_test.cub -my_nparts 4 -output_file sphere_test_4.h5m
while mofem_part can be found in $HOME/mofem_install/um/build_release/tools/. Here we partitioned the mesh in 4 parts in order to be executed on 4 cores in a distributed-memory parallel environment. Note that any number of parts less or equal to number of physically available cores can be used.
Stokes equation
mpirun -np 4 ./navier_stokes -my_file sphere_test_4.h5m \
-my_order_u 2 \
-my_order_p 1 \
-my_discont_pressure 0 \
-my_num_ho_levels 1 \
-my_ho_geometry 1 \
-my_step_num 1 \
-my_velocity_scale 0.1 \
-my_length_scale 2 \
-my_stokes_flow 1 \
-my_is_partitioned 1
Navier-Stokes equations
mpirun -np 4 ./navier_stokes -my_file sphere_test_4.h5m \
-my_order_u 2 \
-my_order_p 1 \
-my_discont_pressure 0 \
-my_num_ho_levels 1 \
-my_ho_geometry 1 \
-my_step_num 2 \
-my_velocity_scale 0.1 \
-my_length_scale 2 \
-my_stokes_flow 0 \
-my_is_partitioned 1



